dask_sparse_mtx

Overview

This is a simple demo showing how to use dask delayed and dask arrays to multiply sparse matricies loaded in lazily into memory (here, from an sqlite3 database).

Either approach uses dask.delayed to wrap reading tiles of the matrix into tasks, and then either manually (using dask_sparse_mtx.dask_delayed_mult()) or using the infrastructure provided by dask.array (using dask_sparse_mtx.dask_array_mult()) multiplies the two matrices in a tiled manner:

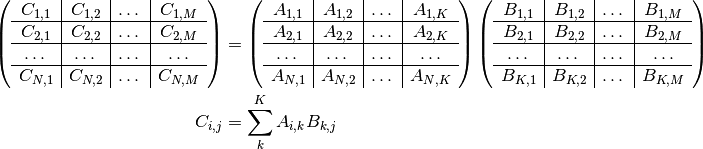
\left( \begin{array}{c|c|c|c} C_{1,1} & C_{1,2} & \dots & C_{1,M} \\ \hline C_{2,1} & C_{2,2} & \dots & C_{2,M} \\ \hline \dots & \dots & \dots & \dots \\ \hline C_{N,1} & C_{N,2} & \dots & C_{N,M} \\ \end{array} \right ) & = \left( \begin{array}{c|c|c|c} A_{1,1} & A_{1,2} & \dots & A_{1,K} \\ \hline A_{2,1} & A_{2,2} & \dots & A_{2,K} \\ \hline \dots & \dots & \dots & \dots \\ \hline A_{N,1} & A_{N,2} & \dots & A_{N,K} \\ \end{array} \right ) \left( \begin{array}{c|c|c|c} B_{1,1} & B_{1,2} & \dots & B_{1,M} \\ \hline B_{2,1} & B_{2,2} & \dots & B_{2,M} \\ \hline \dots & \dots & \dots & \dots \\ \hline B_{K,1} & B_{K,2} & \dots & B_{K,M} \\ \end{array} \right ) C_{i,j} & = \sum_{k}^K A_{i,k} B_{k,j}

where the multiplication in the second line above is matrix multiplication.

The example can be run as follows (will take a few minutes):

import os
import dask.multiprocessing
import dask_sparse_mtx as dsm

dask.set_options(get=dask.multiprocessing.get)

filename = "test.db"
size = 20000

# create file
dsm.mtxdb_init(filename)

# create matrices and write them; their product
# will be the identity matrix
a = dsm.mtx_permutation(size)
b = dsm.mtx_transpose(a)
dsm.mtxdb_add_matrix_from_dict(filename, 'A', a)
dsm.mtxdb_add_matrix_from_dict(filename, 'B', b)

# smaller tilesize - more parallelism, but more
# overhead from task management
tilesize = 2000
c = dsm.dask_array_mult(filename, 'A', 'B', tilesize)

print c[:10, :10]

if dsm.mtx_is_identity(c):
    print "Success!"

os.remove(filename)

And using dask.distributed this computation can be run across several hosts.

Matrix Multiplication

Matrix multiplication is performed by either dask_sparse_mtx.dask_delayed_mult() or dask_sparse_mtx.dask_array_mult():

Multiply two sparse matrices in the database

using dask.delayed and task parallelism.

Pros: high control over tiles size, distribution Cons: larger memory usage in intermediate steps as

tiles can’t be mutated
dask_sparse_mtx.dask_delayed_mult.dask_delayed_mult(dbname, a, b, tilesize)

Multiplies two sparse matrices from the matrix db using dask.delayed and task parallelism

TODO: better reduction over intermediate terms

Parameters:
  • dbname – Filename of the sparse matrix db
  • a – Name of matrix A in the db
  • b – Name of matrix B in the db
  • tilesize – int - size of the (square) tiles read in to do the multiplication
Return type:

dictionary of sparse.COO matrix tiles - eg c[(i,j)] is the i, jth tile of product
Multiply two sparse matrices in the database

by constructing a dask array from the tiles

Pros: Makes better use of the scheduler, esp for large numbers of tiles
Don’t have to think about de-tiling final result

Cons: Less control of tiling in intermediate and final stages

dask_sparse_mtx.dask_array_mult.dask_array_mult(dbname, a, b, tilesize)

Multiplies two sparse matrices from the matrix db using dask.arrays

Parameters:
  • dbname – Filename of the sparse matrix db
  • a – Name of matrix A in the db
  • b – Name of matrix B in the db
  • tilesize – int - size of the (square) tiles read in to do the multiplication
Return type:

sparse.COO - single sparse matrix final result

Sparse Matrix DB

These rely on routines for reading/writing the sparse matrices (in COO format) into the sqlite3 db:

Reads/writes sparse matrices (in COO format) into
sqlite3 db
dask_sparse_mtx.mtxdb.mtxdb_init(filename)

Initializes an sqlite3 db for writing sparse matrices.

Parameters:filename – name of sqlite3 db file to create
dask_sparse_mtx.mtxdb.mtxdb_add_matrix_from_dict(filename, mtxname, mtxdict)

Writes a matrix in COO format to sqlite3 db ‘filename’.

Parameters:
  • filename – name of sqlite3 db in which to store the matrix
  • mtxname – name of matrix (string)
  • mtxdict – dict of form (row, col): value containing matrix coordinates and data
dask_sparse_mtx.mtxdb.mtxdb_read_chunk(filename, mtxname, rows=None, cols=None)
Reads a whole or partial matrix from a sqlite3 db into
a mod:sparse COO matrix
Parameters:
  • filename – name of sqlite3 db from which to read the matrix
  • mtxname – name of matrix (string)
  • rows – optional tuple containing the slice of rows to read in, eg rows=(100,200) will read in rows 100..199. If None, will read all rows
  • cols – as with rows, but for columns
Return type:

mod:sparse COO matrix
dask_sparse_mtx.mtxdb.mtxdb_matrix_shape(filename, mtxname)

Returns the shape of a sparse matrix in the db.

Parameters:
  • filename – name of the sqlite3 db in which the matrix is stored
  • mtname – name of the matrix(string)
Return type:

(rowmin, rowmax, colmin, colmax): min/max of rows and columns

Sparse Matrix Helper Methods

And finally there are helper routines for creating simple permutation matricies useful for tests:

Routines for simple COO matrices expressed as dicts
{(row, col): value } for test problems
dask_sparse_mtx.mtx.mtx_permutation(size)

Returns a matrix in COO format as a dictionary describing a permutation matrix.

Parameters:size – size of (necessarily square) permutation matrix
Return type:dictionary of (row, col): val matrix entries
dask_sparse_mtx.mtx.mtx_transpose(dictmtx)

Returns transposes of a matrix in COO format (expressed as a dict).

Parameters:dictmtx – dictionary containing COO matrix
Return type:dictionary of (row, col): val matrix entries
dask_sparse_mtx.mtx.mtx_is_identity(mtx)

Returns True if matrix (dict or sparse.COO) is the identity matrix False otherwise

Parameters:mtx – sparse.COO or dict matrix
Return type:Bool: True if identity

Indices and tables